프로그래머스] C++ 연습문제 - 스티커 모으기(2) (level 4)

해당 문제는 프로그래머스 코딩테스트 연습에 있는 문제입니다.

아래 링크를 통해 풀 수 있습니다.

https://programmers.co.kr/learn/courses/30/lessons/12971

1. 문제

N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.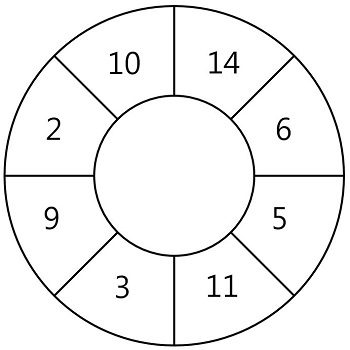

원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.

예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

제한 사항

• sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
• sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
• 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

---

입출력 예

sticker	answer
[14, 6, 5, 11, 3, 9, 2, 10]	36
[1, 3, 2, 5, 4]	8

입출력 예 설명

입출력 예 #1
6, 11, 9, 10이 적힌 스티커를 떼어 냈을 때 36으로 최대가 됩니다.

입출력 예 #2
3, 5가 적힌 스티커를 떼어 냈을 때 8로 최대가 됩니다.

2. 조건

1. 숫자를 하나 선택하면 양 옆에 있는 숫자는 선택할 수 없다.

2. 이런 조건일 때 모든 합의 최대 값을 구하여라.

3. 풀이

해당문제는 dp(dynamic programming)로 풀어야 합니다.

dp의 조건은 다음과 같이 세울 수 있습니다.

dp[i] = max(dp[i - 1], dp[i - 2] + sticker[i]);

왜이렇게 되는지 설명해 하겠습니다.

(A4용지같은 빈 공간에 일일이 적어가면서 직접 보는것이 제일 이해하기 쉽습니다.)

우선 저희는 최대 합을 구해야 합니다.

합에 집중해 봅시다.

만약 제가 첫번째를 선택했다면 다음 그림과 같은 선택권이 있을 것입니다.

파란색 부분인 14를 선택하면 빨간색 부분을 모두 택할 수 있습니다.

하지만 우리는 최대 합을 구해야 합니다.

그럼 14에서 2가지 선택을 할 수 있습니다.

5를 선택하던지 11을 선택하던지.

왜 이 2개를 선택하느냐?

5를 선택할 경우 5의 오른쪽인 11을 선택 못하게 됩니다.

반대로 11을 선택할 경우 5와 3을 선택 못하게 되죠.

즉, 5를 선택하느냐 11을 선택하느냐에 따라 값이 달라지게 됩니다.

5와 11중 더했을 때 값이 큰것을 dp[]배열에 저장합니다.

그 다음 11과 3을 비교합니다. 이것을 반복하면 됩니다.

그럼 두가지 의문점이 들것입니다.

1. 5나 11로 안가고 3이나 9로 가도 되지 않느냐?

2. 5랑 11중 최대 값인 11 더한 값을 dp[]에 넣었는데 11 옆에 있는 값이 1000이라면 이건 잘못되지 않았느냐?

1번에 대한 답은 다음과 같습니다.

저희는 최대 합을 구해야 합니다. 때문에 최대한 많은 숫자를 더해야 하기 때문에 더할 수 있는 가장 가까운 두수를 선택한 것입니다.

2번에 대한 답은 다음과 같습니다.

dp 계산식을 보면 아시겠지만  max(dp[i - 1], dp[i - 2] + sticker[i]); 입니다.

즉, i를 증가 시키면서 비교하므로 11 옆에있는 3도 비교하게 됩니다.

대신 비교를 할 때 11을 더했을 때 값이 크냐? 3을 더했을 때 값이 크냐에 따라 dp값이 저장이 되고,

만약 작은 값이 있을 경우에는 처음시작점 부터 동일한 원리로 작동되는걸 말씀드리겠습니다.

dp[4] 부분을 보시면 같은 숫자가 나왔습니다.

이는 max()부분에서 전 값이 더 크기 때문에 이렇게 된 것입니다.

첫 부분인 14, 14로 시작하는 것과, 전 값이 더 크기 때문에 나온 25, 25 부분은 같다고 보시면 됩니다.

잊지 말아야 할점은 저희는 최대 합을 구하는 것입니다. 

때문에 전 값이 큰 부분이 나왔다면 그 구간의 최대 값은 25인 샘입니다.

그럼 25지점부터 다시 25부터 두칸 떨어진 부분과 세칸 떨어진 부분의 최대 합을 구해나가면 됩니다.

여기서 두칸과 세칸이라 표시했지만 dp에 저장되는 값 특성상 i-1과 i-2가 됩니다.

이점 유의하면서 dp를 직접 돌려보시면 될 것입니다.

또한 중요한 점은 이 문제를 해결할 때 첫 지점을 정하는 것입니다.

14를 정할 때는 맨 끝부분인 10을 더하지 못합니다.

따라서 10을 더할 수 있는 즉, 14가 아닌 6부터 시작하는 dp를 추가로 생성해줘야 한다는 뜻입니다.

코드는 아래와 같습니다.

4. 코드

#include <iostream>

#include <vector>

using namespace std;

int solution(vector<int> sticker)

{

    int answer = sticker[0];

    int dp1[100002] = { 0, };

    int dp2[100002] = { 0, };

    

    dp1[0] = dp1[1] = sticker[0];

    dp2[0] = 0, dp2[1] = sticker[1];

    

    for(size_t i = 2; i < sticker.size(); i++){

        if(i != sticker.size() - 1) {

            dp1[i] = max(dp1[i - 2] + sticker[i], dp1[i - 1]);

            answer = dp1[i];

        }

        dp2[i] = max(dp2[i - 2] + sticker[i], dp2[i - 1]);

    }

    answer = max(answer, dp2[sticker.size() - 1]);

    return answer;

}